Кинематика станка-качалки
Кинематическая схема преобразующего механизма балансирного станка-качалки представляет четырехзвенник OBCD (рис. 4.35.). Неподвижное звено - OD (расстояние от О до D), подвижные звенья - кривошип r, шатун l и заднее плечо балансира b.
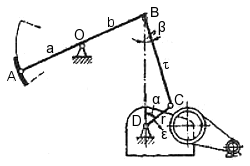
Рис. 4.35. Кинематическая схема балансирного станка-качалки
При вращении кривошипа точка С описывает окружность радиуса r, а точка В
движется по дуге радиуса b.
Для упрощения определения закона
движения точки В в расчетах делают некоторые допущения, а именно:
- точка В движется не по дуге, а по прямой;
- принимают r/l = 0; r/b = 0, т. е. считают, что радиус кривошипа намного меньше длины балансира;
- угол β, образованный шатуном и линией, соединяющей центр кривошипа, с точкой В, принимают равным нулю.
В этом случае закон движения точки В соответствует закону движения поршня насоса с кривошипно-шатунным механизмом.
При уточненных расчетах учитывают конечную длину шатуна, так как при значительной длине хода (4,5...6 м) отношение радиуса кривошипа к длине шатуна r/l становится значительной величиной. Однако и в этом случае делают допущение, считая, что траектория движения точки В прямолинейна.
При точных расчетах учитывают и кривизну траектории движения точки В, что позволяет уменьшить погрешность расчета.
Найдем закон движения точки подвеса штанг, т. е. определим путь, скорость и ускорение точки В во времени.
Путь S, пройденный точкой В при повороте кривошипа на угол α (точка В займет новое положение В1), равен:
SB = B1B = BD — B1D,
тогда ВD будет равно r + l, а из треугольника BCD следует B1D = r · cosα + l ·cosβ, откуда:
SB = r + l — r · cosα — l · cosβ = r · (1 — cosα) + l · (1 — cosβ),
С учетом допущений, принятых в элементарной теории, что β = 0, будем иметь:
SB = r · (1 — соsα). (4.15)
Скорость движения точки В будет равна:
νB = ω · r · sinα, (4.16)
а ускорение:
wB = ω2 · r · cosα (4.17)
Путь, скорость и ускорение точки А определяются соотношением плеч балансира а и b:
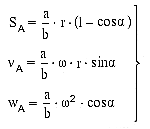 (4.18)
(4.18)
здесь ω - угловая скорость вращения кривошипа.
Графики изменения скорости и ускорения точки подвеса колонны штанг — это синусоида и косинусоида соответственно. Графическое изображение см. аналогично рис. 1.2.
Более точно закономерность изменения перемещения, скорости и ускорения точки подвеса штанг может быть определена с помощью приближенной теории (приближенного расчета).
Кинематическое совершенство станка-качалки характеризуется коэффициентом:
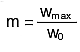
где wmax - максимальное ускорение точки подвеса штанг
станка-качалки, определяемое по точной теории,
w0 - ускорение при
гармоничном движении.
Для определения показателя m удобно пользоваться следующей формулой:
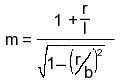 (4.19)
(4.19)
В зависимости от глубины подвески насоса допустимый коэффициент
кинематического совершенства изменяется и для глубоких скважин должен быть m ≤
1,3.

